对于有向图，在其每一个强连通分量中，任何两个顶点都是可达的。设V为G的顶点，与V可相互到达的所有顶点就是包涵V的强连通分量的所有顶点。

 

设从V可到达（以V为起点的所有有向路径的终点）的 顶点集合为T1（G）,二到达V（以V为终点的所有有向路径的起点）的顶点集合为T2(G)，则包含V的强连通分量的顶点集合是：

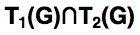
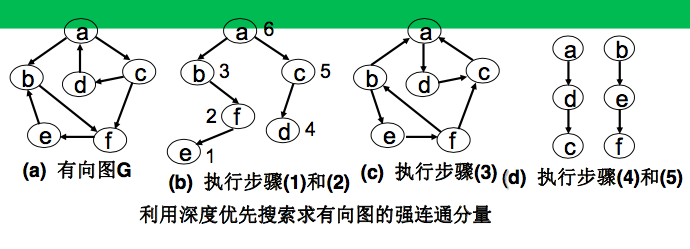
求有向图G的强连通分量的基本步骤是：

（1）对G进行深度优先遍历，生成G的深度优先生成森林T。

（2）对森林T的顶点按中序遍历顺序进行编号。

（3）改变G中每一条弧的方向，构成一个新的有向图G‘。

（4）按（2）中标出的顶点编号，从编号最大的顶点开始对G‘ 进行深度优先搜索，得到一棵深度优先生成树。若一次完整的搜索过程没有遍历G'的所有顶点，中则从未访问过的顶点中选择一个编号最大的顶点，由它开始再进行深度优先搜索，并得到另一棵深度优先生成树。在该步骤中，每一次深度优先搜索得到的生成树中的顶点就是G的一个强连通分量的所有顶点。

（5）repeat（4）。till end

算法实现：

 在算法实现是，建立一个数组in_order[n]存放深度优先森林的中序遍历序列。对每个顶点v在调用DFS函数结束时，将顶点依次存放在数组in_order[n]中。采用十字链表作为储存结构。

int in_order[MAX_VEX];void DFS(OLGraph *G, int v)  //按弧的正向搜索{	ArcNode *p;	count = 0;	visited[v] = true;  //visited数组，判断是否第二次访问	for(p = G->xlist[v].firstout; p != NULL ; p=p->tlink)		if(!visited[p->headvex])			DFS(G, p->headvex);	in_order[count++]=v;}void Rex_DFS(OLGraph *G, int v)  //按弧的逆向搜索{    ArcNode *p;    visited[v] = true;    printf("%d",v);  //输出顶点    for(p=G->xlist[v],firstin; p!=NULL; p=p->hlink)    	if(!visited[p->tailvex])    		Rex_DFS(G, p->tailvex);}void Connected_DG(OLGraph *G){	int k=1, v, j;	for(int v=0; v < G->vexnum ; v++)		visited[v] = false;	for(v = 0;v
     
      vexnum; v++)  //对图G正向遍历		if(!visited[v]) DFS(G, v);	for(v = 0;v
      
       vexnum;v++)		visited[v] = false;//对图逆向遍历	for(j=G->vexnum-1; j>=0; j--)	{		v=in_order[j];		if(!visited[v])		{			printf("\n第%d个连通分量顶点：", k++);			Rex_DFS(G, v);		}	}}